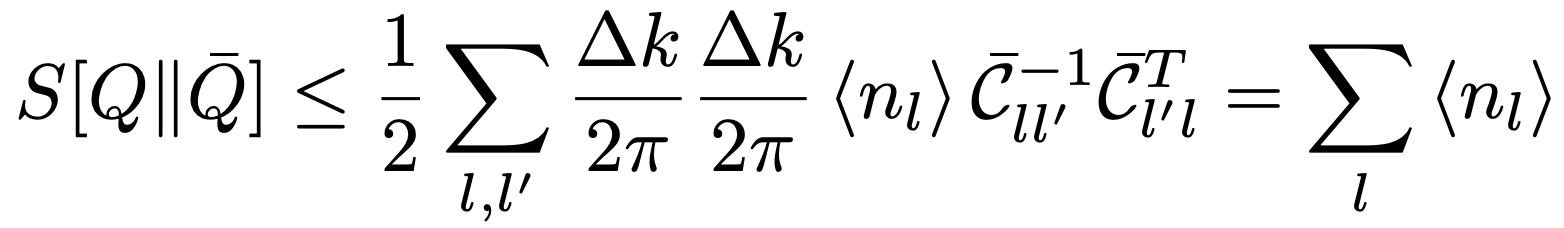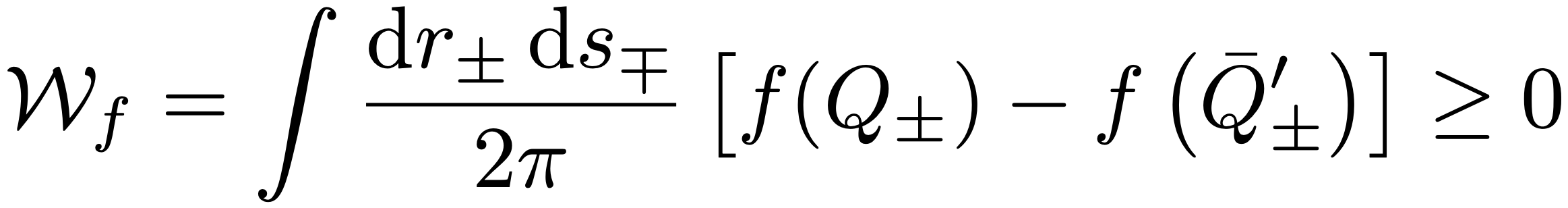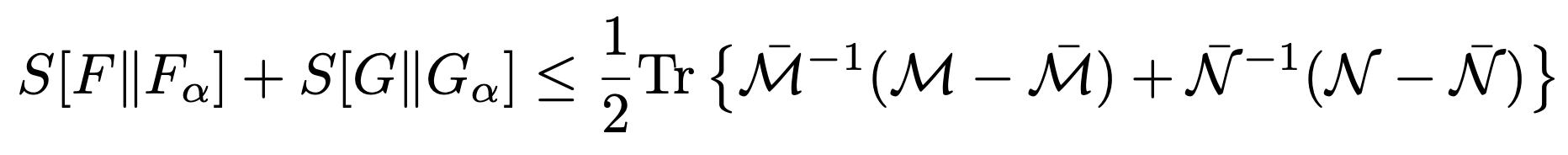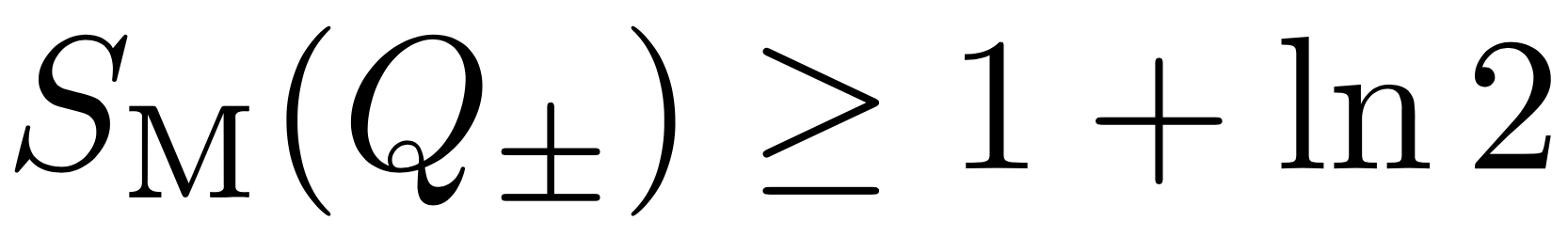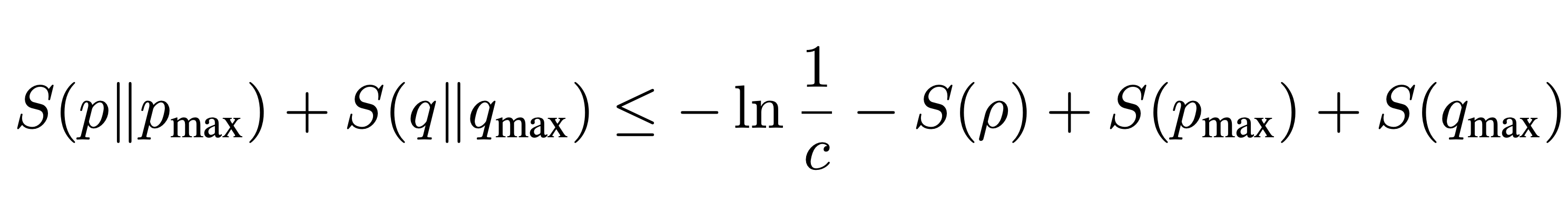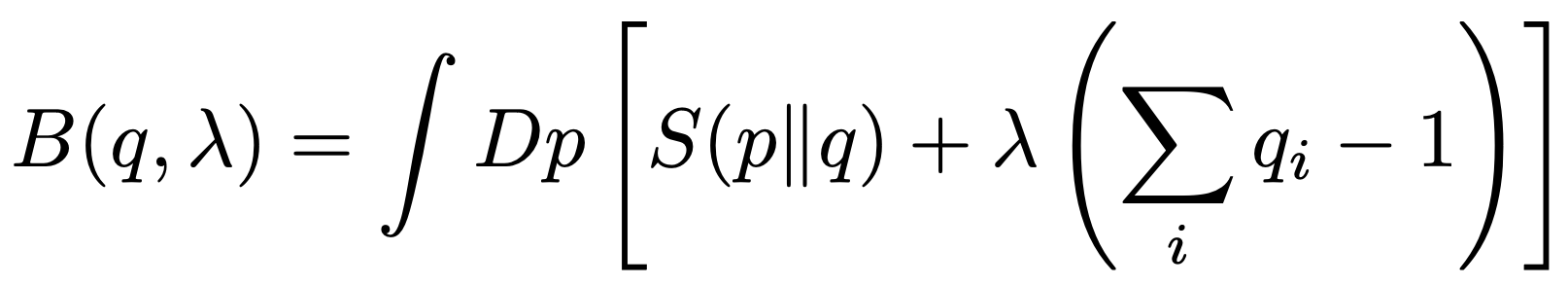Publications
In principle you can find all my publications on
arXiv. Moreover, my orcid-ID is
0000-0003-1477-9855. Below all publications are listed in chronological order (beginning with the most recent one) together with their respective abstracts.
Preprints
- 07/23: Entropic distinguishability of quantum fields in phase space with Sara Ditsch.
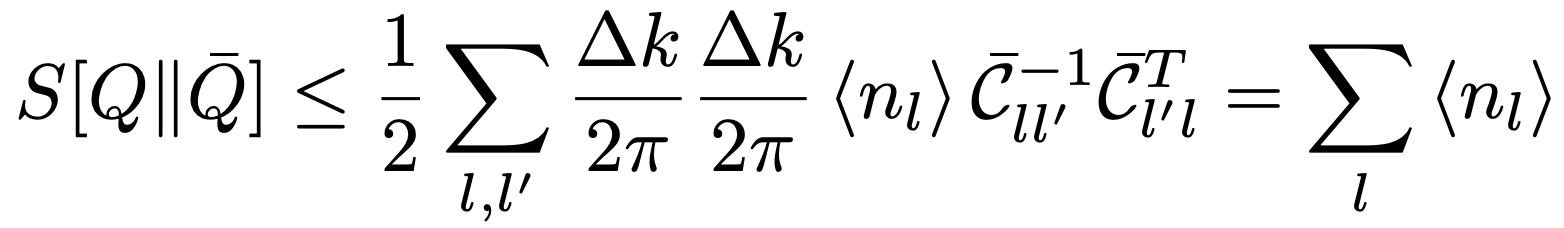
We present a general way of quantifying the entropic uncertainty of quantum field configurations in field-theoretic phase space in terms of entropic distinguishability. Our approach is based on the functional Husimi Q-distribution and a suitably chosen relative entropy thereof, which we show to be non-trivially bounded from above by the uncertainty principle. The resulting relative entropic uncertainty relation holds for a finite number of modes as well as for quantum fields and is as general as the concept of coherent states. We evaluate this relation for bosonic and fermionic degrees of freedom by considering the relativistic scalar field and the spinless Majorana fermion, respectively. We find that the bound on the entropic distinguishability of excitations with respect to the vacuum scales with the average number of excitations and is independent of the particle nature.
- 05/23: Accessing continuous-variable entanglement witnesses with multimode spin observables with Célia Griffet and Nicolas Cerf.

We present several measurement schemes for accessing separability criteria for continuous-variable bipartite quantum systems. Starting from moments of the bosonic mode operators, criteria suitable to witness entanglement are expressed in terms of multimode spin observables via the Jordan-Schwinger map. These observables are typically defined over a few replicas of the state of interest and can be transformed into simple photon-number measurements by passive optical circuits. Our measurement schemes require only a handful of measurements, thereby allowing one to efficiently detect entanglement without the need for costly state tomography as illustrated for a variety of physically relevant states (Gaussian, mixed Schrödinger cat, and NOON states). The influence of typical experimental imperfections is shown to be moderate.
- 12/22: General class of continuous variable entanglement criteria with Martin Gärttner and Johannes Noll.
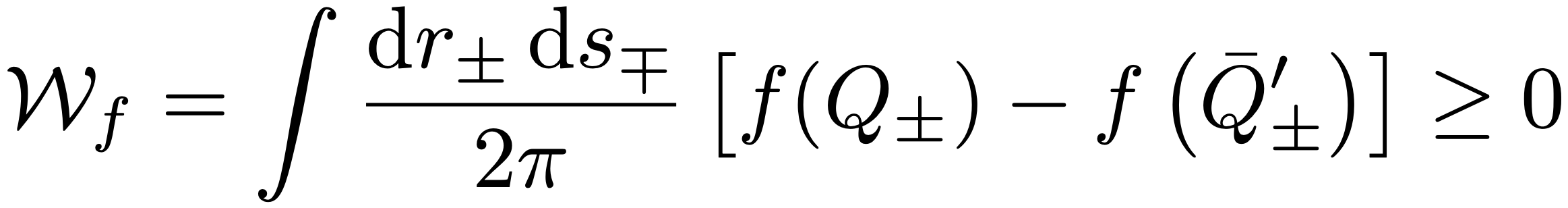
We present a general class of entanglement criteria for continuous variable systems. Our criteria are based on the Husimi Q-distribution and allow for optimization over the set of all concave functions rendering them extremely general and versatile. We show that several entropic criteria and second moment criteria are obtained as special cases. Our criteria reveal entanglement of families of states undetected by any commonly used criteria and provide clear advantages under typical experimental constraints such as finite detector resolution and measurement statistics.
- 12/22: Detecting continuous variable entanglement in phase space with the Q-distribution with Martin Gärttner and Johannes Noll.

We prove a general class of continuous variable entanglement criteria based on the Husimi Q-distribution, which represents a quantum state in canonical phase space, by employing a theorem by Lieb and Solovej. We discuss their generality, which roots in the possibility to optimize over the set of concave functions, from the perspective of continuous majorization theory and show that with this approach families of entropic as well as second moment criteria follow as special cases. All derived criteria are compared to corresponding marginal based criteria and the strength of the phase space approach is demonstrated for a family of prototypical example states where only our criteria flag entanglement.
- 12/22: Optimizing detection of continuous variable entanglement for limited data with Martin Gärttner and Johannes Noll.

We explore the advantages of a class of entanglement criteria for continuous variable systems based on the Husimi Q-distribution in scenarios with sparse experimental data. The generality of these criteria allows optimizing them for a given entangled state and experimental setting. We consider the scenario of coarse grained measurements, or finite detector resolution, where the values of the Husimi Q-distribution are only known on a grid of points in phase space, and show how the entanglement criteria can be adapted to this case. Further, we examine the scenario where experimental measurements amount to drawing independent samples from the Husimi distribution. Here, we customize our entanglement criteria to maximize the statistical significance of the detection for a given finite number of samples. In both scenarios optimization leads to clear improvements enlarging the class of detected states and the signal-to-noise ratio of the detection, respectively.
Published Papers
- 11/22: Quantum field simulator for dynamics in curved spacetime with Celia Viermann, Marius Sparn, Nikolas Liebster, Maurus Hans, Elinor Kath, Álvaro Parra-López, Mireia Tolosa-Simeón, Natalia Sánchez-Kuntz, Helmut Strobel, Stefan Flörchinger and Markus K. Oberthaler.

The observed large-scale structure in our Universe is seen as a result of quantum fluctuations amplified by spacetime evolution. This, and related problems in cosmology, asks for an understanding of the quantum fields of the standard model and dark matter in curved spacetime. Even the reduced problem of a scalar quantum field in an explicitly time-dependent spacetime metric is a theoretical challenge and thus a quantum field simulator can lead to new insights. Here, we demonstrate such a quantum field simulator in a two-dimensional Bose-Einstein condensate with a configurable trap and adjustable interaction strength to implement this model system. We explicitly show the realisation of spacetimes with positive and negative spatial curvature by wave packet propagation and confirm particle pair production in controlled power-law expansion of space. We find quantitative agreement with new analytical predictions for different curvatures in time and space. This benchmarks and thereby establishes a quantum field simulator of a new class. In the future, straightforward upgrades offer the possibility to enter new, so far unexplored, regimes that give further insight into relativistic quantum field dynamics.
- 09/22: Curved and expanding spacetime geometries in Bose-Einstein condensates with Mireia Tolosa-Simeón, Álvaro Parra-López, Natalia Sánchez-Kuntz, Celia Viermann, Marius Sparn, Nikolas Liebster, Maurus Hans, Elinor Kath, Helmut Strobel, Markus K. Oberthaler and Stefan Flörchinger.

Phonons have the characteristic linear dispersion relation of massless relativistic particles. They arise as low energy excitations of Bose-Einstein condensates and, in nonhomogeneous situations, are governed by a space- and time-dependent acoustic metric. We discuss how this metric can be experimentally designed to realize curved spacetime geometries, in particular, expanding Friedmann-Lemaître-Robertson-Walker cosmologies, with negative, vanishing, or positive spatial curvature. A nonvanishing Hubble rate can be obtained through a time-dependent scattering length of the background condensate. For relativistic quantum fields this leads to the phenomenon of particle production, which we describe in detail. We explain how particle production and other interesting features of quantum field theory in curved spacetime can be tested in terms of experimentally accessible correlation functions.
- 05/22: Scalar quantum fields in cosmologies with 2+1 spacetime dimensions with Natalia Sánchez-Kuntz, Álvaro Parra-López, Mireia Tolosa-Simeón and Stefan Flörchinger.

Motivated by the possibility to use Bose-Einstein condensates as quantum simulators for spacetime curvature, we study a massless relativistic scalar quantum field in spatially curved Friedmann-Lemaître-Robertson-Walker universes with d=2+1 spacetime dimensions. In particular, we investigate particle production caused by a time-dependent background geometry, by means of the spectrum of fluctuations and several two-point field correlation functions. We derive new analytical results for several expansion scenarios.
- 03/22: Relative entropic uncertainty relation for scalar quantum fields with Markus Schröfl and Stefan Flörchinger.
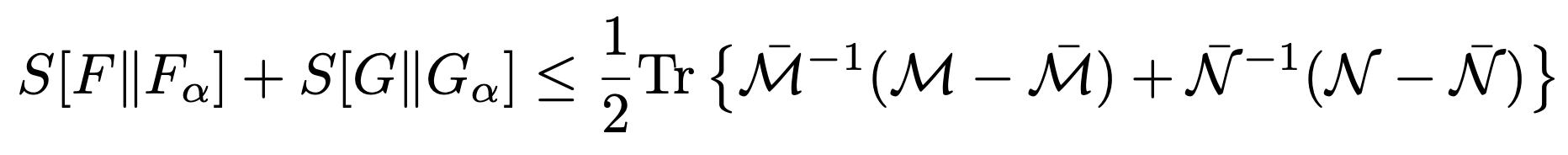
Entropic uncertainty is a well-known concept to formulate uncertainty relations for continuous variable quantum systems with finitely many degrees of freedom. Typically, the bounds of such relations scale with the number of oscillator modes, preventing a straight-forward generalization to quantum field theories. In this work, we overcome this difficulty by introducing the notion of a functional relative entropy and show that it has a meaningful field theory limit. We present the first entropic uncertainty relation for a scalar quantum field theory and exemplify its behavior by considering few particle excitations and the thermal state. Also, we show that the relation implies the multidimensional Heisenberg uncertainty relation.
- 01/22: Entropic entanglement criteria in phase space with Oliver Stockdale, Martin Gärttner and Stefan Flörchinger.
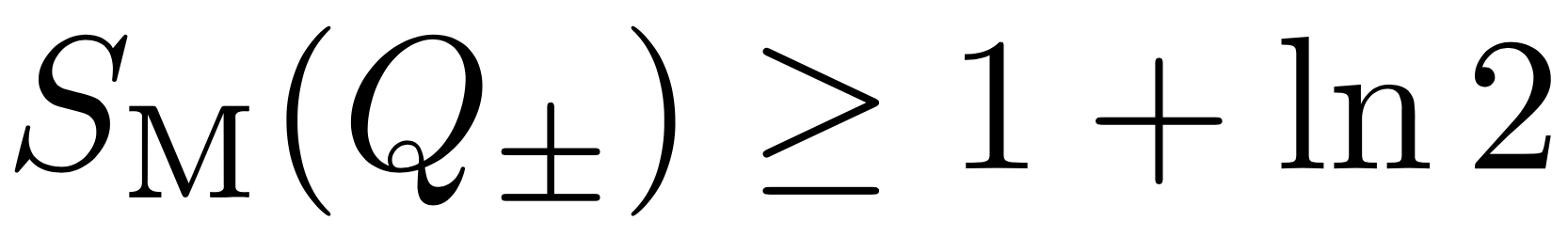
We derive entropic inseparability criteria for the phase-space representation of quantum states. In contrast to criteria involving differential entropies of marginal phase-space distributions, our criteria are based on a joint distribution known as the Husimi Q distribution. This distribution is experimentally accessible in cold atoms, circuit QED architectures, and photonic systems, and bears practical advantages compared to the detection of marginals. We exemplify the strengths of our entropic approach by considering several classes of non-Gaussian states where second-order criteria fail. We show that our criteria certify entanglement in previously undetectable regions, highlighting the strength of using the Husimi Q distribution for entanglement detection.
- 06/21:
Wehrl entropy, entropic uncertainty relations and entanglement witnessing with Henrik Müller-Groeling and Stefan Flörchinger.
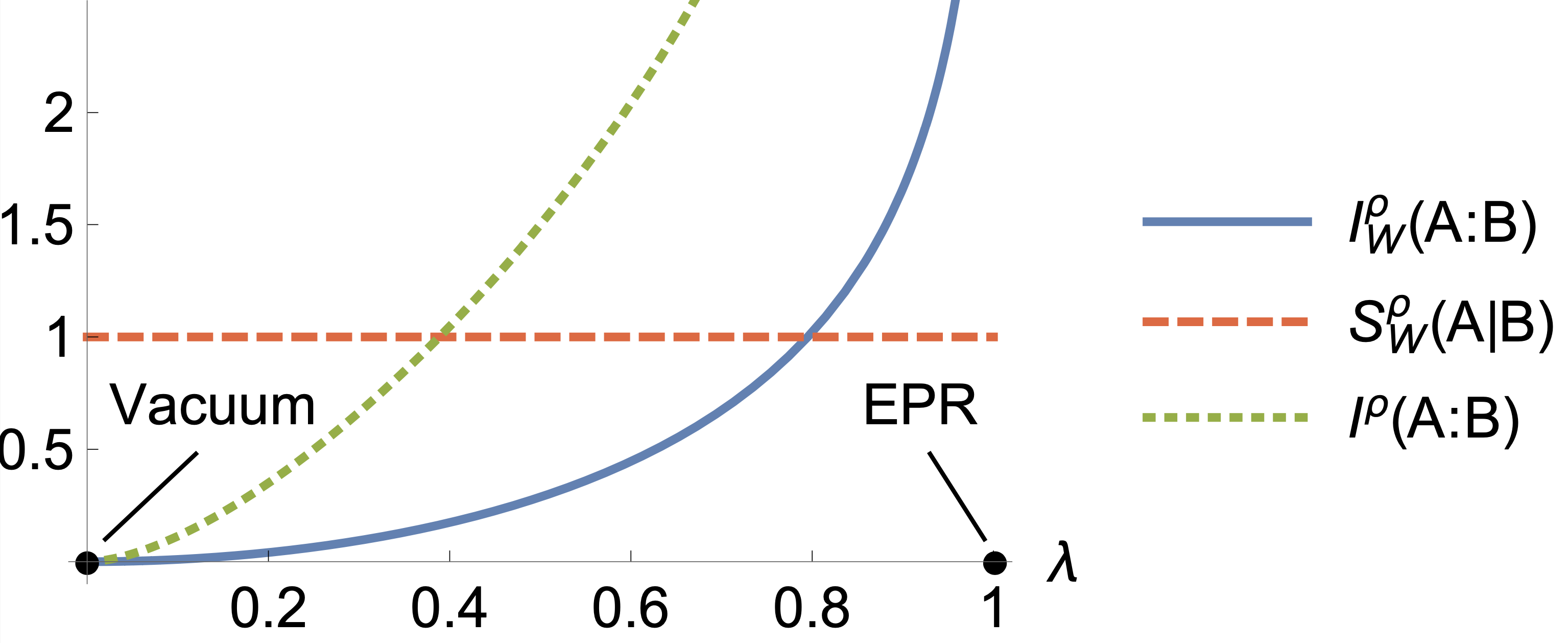
The Wehrl entropy is an entropy associated to the Husimi quasi-probability distribution. We discuss how it can be used to formulate entropic uncertainty relations and for a quantification of entanglement in continuous variables. We show that the Wehrl-Lieb inequality is tighter than the usual Białynicki-Birula and Mycielski entropic uncertainty relation almost everywhere. Furthermore, we show how a Wehrl mutual information can be used to obtain a measurable perfect witness for pure state bipartite entanglement, which additionally provides a lower bound on the entanglement entropy.
- 06/21:
Relative entropic uncertainty relation with Ben Höber and Stefan Flörchinger.
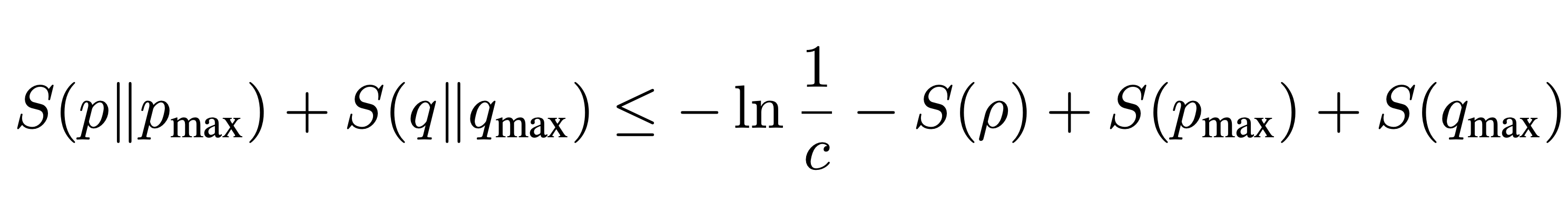
Quantum uncertainty relations are formulated in terms of relative entropy between distributions of measurement outcomes and suitable reference distributions with maximum entropy. This type of entropic uncertainty relation can be applied directly to observables with either discrete or continuous spectra. We find that a sum of relative entropies is bounded from above in a non-trivial way, which we illustrate with some examples.
- 11/20:
Thermodynamics from relative entropy with Stefan Flörchinger.
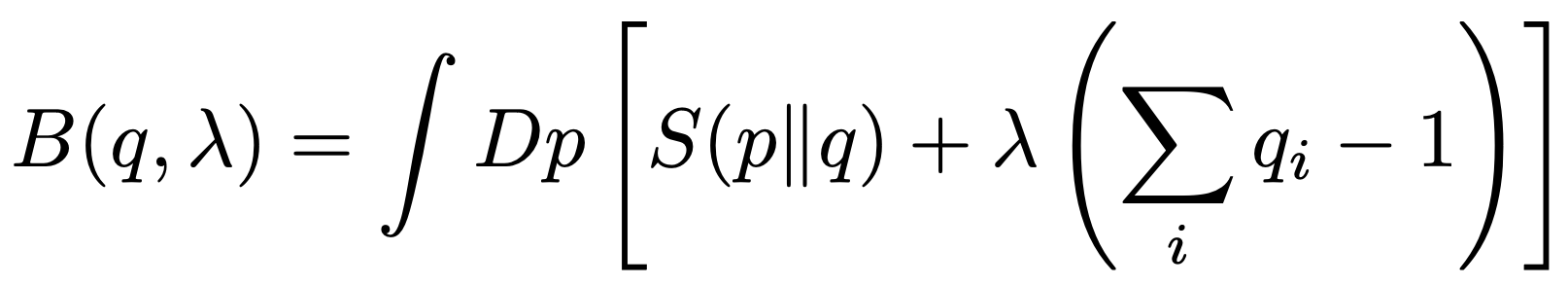
Thermodynamics is usually developed starting from entropy and the maximum entropy principle. We investigate here to what extent one can replace entropy with relative entropy which has several advantages, for example in the context of local quantum field theory. We find that the principle of maximum entropy can be replaced by a principle of minimum expected relative entropy. Various ensembles and their thermodynamic potentials can be defined through relative entropy. We also show that thermal fluctuations are in fact governed by a relative entropy. Furthermore we reformulate the third law of thermodynamics using relative entropy only.
- 11/20: Second law of thermodynamics for relativistic fluids formulated with relative entropy with Neil Dowling and Stefan Flörchinger.
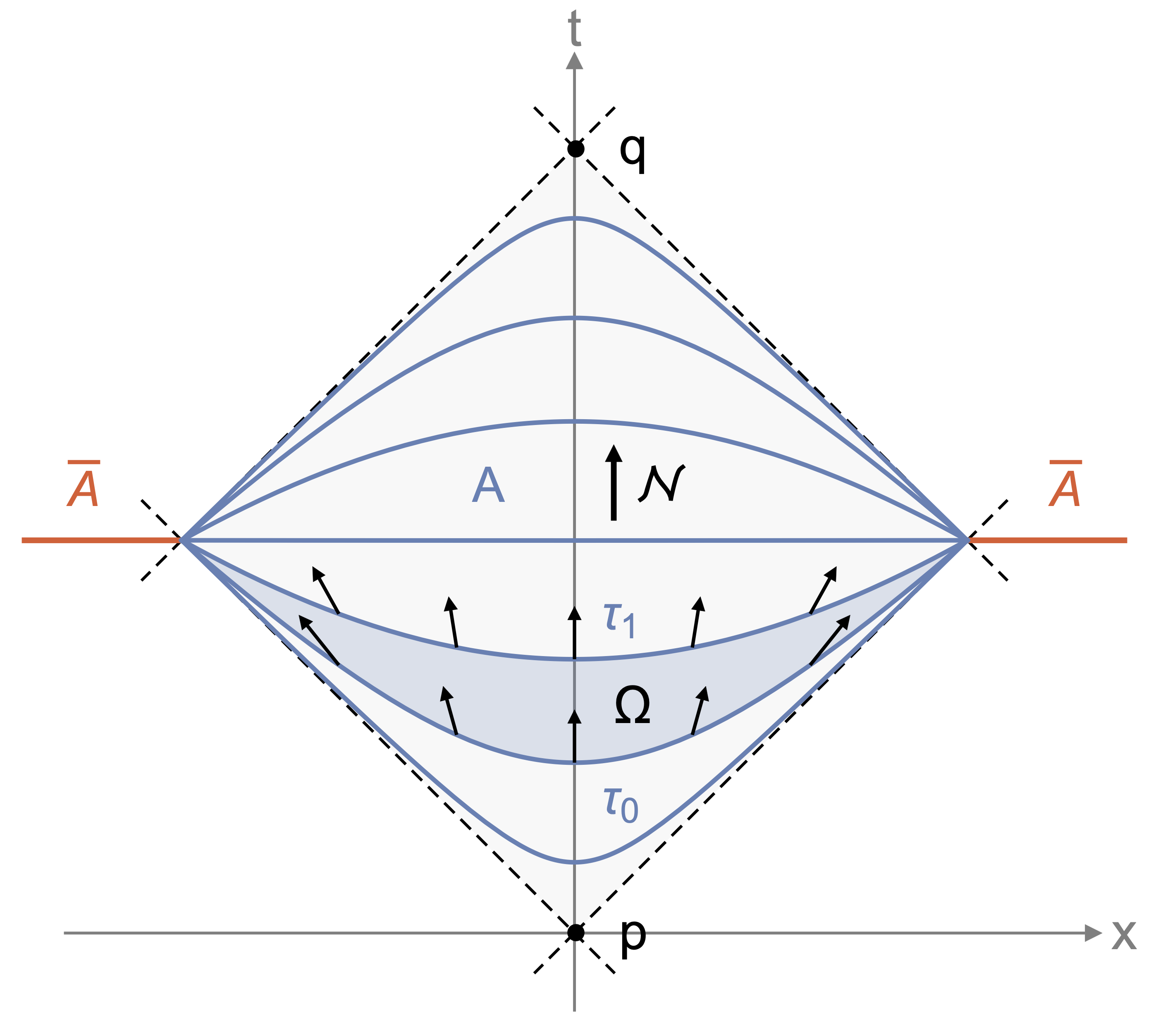
The second law of thermodynamics is discussed and reformulated from a quantum information theoretic perspective for open quantum systems using relative entropy. Specifically, the relative entropy of a quantum state with respect to equilibrium states is considered and its monotonicity property with respect to an open quantum system evolution is used to obtain second law-like inequalities. We discuss this first for generic quantum systems in contact with a thermal bath and subsequently turn to a formulation suitable for the description of local dynamics in a relativistic quantum field theory. A local version of the second law similar to the one used in relativistic fluid dynamics can be formulated with relative entropy or even relative entanglement entropy in a space-time region bounded by two light cones. We also give an outlook toward isolated quantum field theories and discuss the role of entanglement for relativistic fluid dynamics.